Tipos de poligonos en las figuras geometricas

Tipos de poligonos son aquellas  figuras geométricas regulares, convexas y cóncavas. Así como también se conocen polígonos a las estadísticas.

Tipos de poligonos,   son figuras geométricas  limitadas por al menos tres segmentos,

denominados lados.

Los ángulos formados por los lados se denominan vértices.

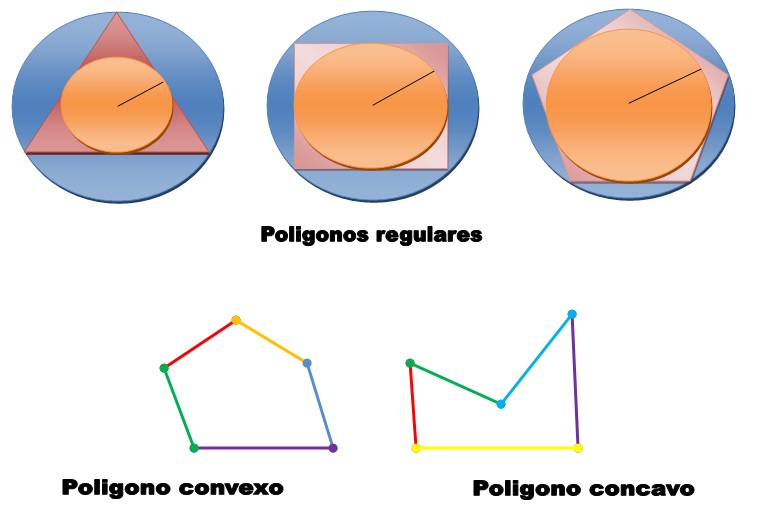
Como he resaltado entre los tipos de polígonos se llama convexos: cuando una recta que contiene un lado deja todos los otros de un mismo lado; en caso contrario se llama cóncavo.

Algunos otros tipos de polígonos son triángulos (si tienen 3 lados), los cuadriláteros ( si tienen 4), pentágonos (si tienen 5 lados), hexágonos ( si tienen 6 ), heptágonos ( si tienen 7), octágonos ( si tienen 8), etc.

Tambien entre los tipos de polígonos pueden ser: Equiángulo, si sus ángulos son iguales, y equilátero, si sus lados son iguales. Si tiene todos los lados y los ángulos iguales, se denomina regular, este puede estar inscrito en una circunferencia y circunscrito en una segunda circunferencia; en el centro común de las dos circunferencias es el centro del polígono.

Para conocer los tipos de polígonos, primero debemos entender que:

El polígono es una figura plana limitada por líneas rectas. Las líneas que delimitan cada uno de los polígonos son las aristas del poliedro, y cada uno de los vértices donde se unen dos aristas son los vértices del poliedro.

Los tipos de polígonos puede ser también caras de un poliedro, es decir son el triangulo regular o equilátero, cuyos ángulos miden 60°; el cuadrilátero regular o cuadro, cuyos ángulos miden 90°, el pentágono regular, el hexágono regular, el heptágono regular, el octágono regular, etc.

A medida que aumenta el número de lados de los tipos de polígonos regulares, crece también la medida de cada uno de los ángulos.

Otros tipos de poligonos son los convexos, y pueden obtenerse sus medidas de la siguiente manera:

El procedimiento aplicado en los tipos de poligonos es el caso de los cuadriláteros se puede aplicar a figuras de más lados. Dado en los tipos de poligonos convexos cualquiera, si se trazan todas las diagonales posibles desde un determinado vértice, quedará dividido en un número de triángulos igual a n -2 donde n nos indica el número de lados del polígono

Una vez que  se sabe el número de triángulos contenidos en  los tipos de  poligonos correspondientes, es fácil deducir que los ángulos internos del polígono sumarán tantas veces 180° como triángulos se compongan. De esta manera, se establece la formula general para calcular la suma S de los ángulos internos de estos tipos de polígonos convexos:

S = 180° * (n-2)

En el caso de de tratarse de tipos de poligonos de seis lados (hexágono), la suma de sus ángulos internos es:

S = 180° * (6=2) = 180° * 3 = 720°

Poligonos regulares y Poligonos irregulares: Convexos y concavos.

Es importante que conozcas otros tipos de poligonos que se usan en estadísticas.

Se elabora a partir de histograma. Consiste en dibujar rectar que unen los puntos medios de la parte superior de los rectángulos obtenidos en el histograma. El poligono de frecuencia se ejemplifica con la siguiente imagen:

1.- Poligono de frecuencias acumuladas:

Para representar estos poligonos se calcula en primer lugar, la frecuencia acumulada de la variable.

2.- Poligono de porcentajes:

El resultado es parecido a los anteriores, pero en este caso los datos que se manejan  son los porcentajes.