Tipos de matrices es el arreglo de números en dos dimensiones (bidimensional)
Son utilizadas para la descripción del sistema de ecuaciones en matemáticas.
Asimismo se usan en aplicaciones para la representación de los coeficientes de las ecuaciones lineales o su representación como datos del vector. Asimismo…
Tipos de matrices cuadrada
Tipos de matrices cuadrada
Como Tipos de matrices en el caso de la cuadrada es la que cuenta con una cantidad de filas igual a la cantidad de columnas.
Los elementos se ubican a partir de la esquina izquierda superior a la esquina derecha inferior, conformando la principal diagonal.
Matrices triangulares:
Tipos de matrices triangulares
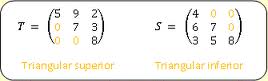
Estos Tipos de matrices (triangulares) muestran una cantidad de filas y columnas diferente, con una dimensión m x n.
Matrices columna:
Una matriz columna es la que se forma solamente por una columna.
Matrices fila:
La matriz fila es formada solamente por una fila.
Matriz diagonal:
Tipos de matrices diagonal
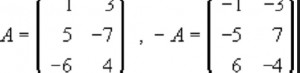
La matriz diagonal se constituye por elementos que se ubican sobre la diagonal y por debajo, siendo de este modo elementos nulos.
Matriz triangular inferior:
En este caso la matriz triangular inferior se caracteriza por sus elementos que se ubican sobre la principal diagonal, siendo los elementos “cero”
Matriz triangular superior:
En la matriz triangular superior, los elementos se ubican debajo de la superior diagonal, siendo los elementos “cero”.
Matriz traspuesta:
Se entiende como matriz traspuesta a la obtenida tras el cambio ordenado de las filas por las columnas.
Matriz identidad:
En la matriz identidad sus elementos en la principal diagonal son iguales a “1”.
Matriz escalar:
Es la matriz diagonal con los elementos iguales en la principal diagonal.
Matriz singular:
La matriz singular simplemente es aquella que carece de inversa.
Matriz regular:
Una matriz regular es la cuadrada que cuenta con inversa.
Por otra parte son triangulares, de identidad, cuadradas y diagonales de acuerdo a la clasificación según el aspecto.
También se puede citar a las:
Matrices ortogonales:
Cuando es cuadrada además de invertible.
Matrices normales:
Si se puede conmutar con su traspuesta.
Dada la íntima relación de las matrices con el sistema de ecuaciones lineales y diferenciales es conveniente que visites tipos de ecuaciones químicas.
De hecho la teoría de matrices indica su multiplicidad de usos con una representación de los coeficientes de sistemas de ecuaciones del tipo lineal y para la representación de aplicaciones lineales.
Inclusive agrega la posibilidad de ser descompuestos, multiplicados y sumados, por ello son aplicables en el álgebra lineal.
Asimismo se puede agregar que los números en el arreglo bidimensional se ordenan en filas (renglones) y columnas.
Una fila representa la línea horizontal de la matriz y la columna se representa con líneas verticales.
Las matrices son denotadas con letras en mayúscula con sus correspondientes letras minúsculas que denotan sus entradas.
Asimismo se pueden denotar con mayúsculas y en negritas para que se puedan diferenciar de otros objetos matemáticos.
A partir de sus aplicaciones es posible realizar con las matrices distintas operaciones, ya sea sumar o restar, gracias a sus propiedades de conmutatividad y asociatividad.
Deja un comentario